Introduction
Pythagorean triples, such as (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25) , (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53) , (11, 60, 61), (33, 56, 65), (48, 55, 73) , (39, 80, 89), (65, 72, 97), have long been recognized for their mathematical elegance. At first glance, these triples appear unordered, and until recently, no method existed to arrange them in a systematic and visually coherent manner.
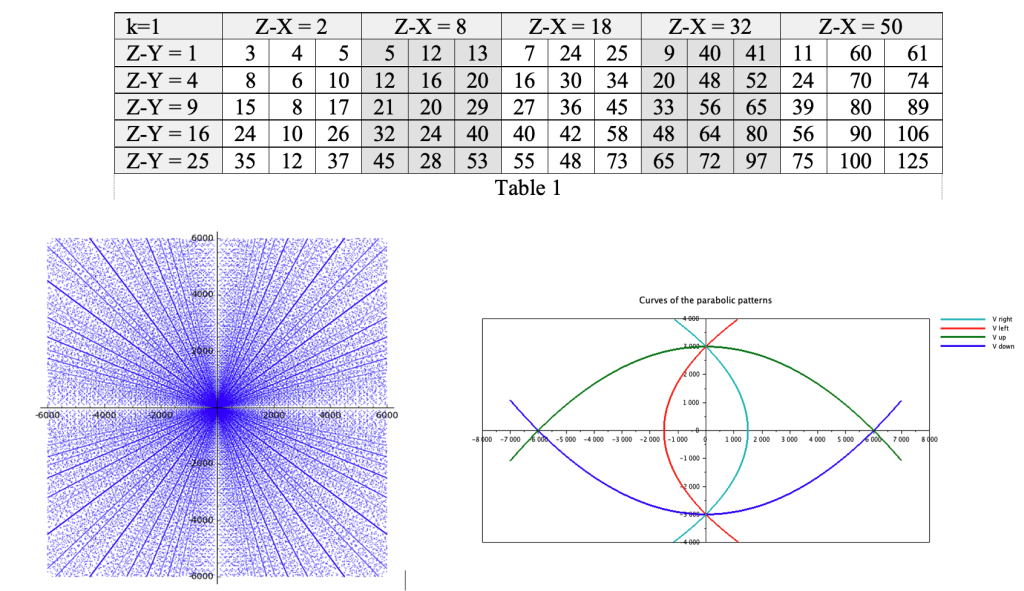
In a previous work, « Classification of Pythagorean triples and reflection on Fermat’s last theorem», we proposed a method for classifying all Pythagorean triples. In this approach, triples are organized into a table in which columns correspond to constant Z−X values and rows correspond to constant Z−Y values Table 1. All the triples listed above appear in this table.
Another approach for representing Pythagorean triples is to plot them as points in a Cartesian coordinate system, with the abscissa and ordinate corresponding to the X and Y values of each triple. When many triples are plotted, the resulting collection of points forms a scatter plot, referred to here as the scatter plot of Pythagorean triples.
An example of such a plot is shown in the Pythagorean triple article on Wikipedia . This scatter plot exhibits striking parabolic patterns, suggesting an underlying geometric order to the triples. The “Distribution of triples ” section of the article describes these patterns as follows:
“Within the scatter, there are sets of parabolic patterns with a high density of points and all their foci at the origin, opening up in all four directions. Different parabolas intersect at the axes and appear to reflect off the axis with an incidence angle of 45 degrees, with a third parabola entering in a perpendicular fashion.”
Although these patterns have been noted, no explanation for their origin has previously been established.
Building upon the theoretical framework developed in « Classification of Pythagorean triples and reflection on Fermat’s last theorem», we derive four explicit parabolic functions from the Pythagorean equation that account for these patterns. The four parabolas plotted in Figure 2 represent these functions. At the intersection points along the Y-axis, the features described above are precisely observed: parabolas intersecting the axes, reflecting at 45 degrees, and intersected perpendicularly by a third parabola.
For more detail, please read «Parabolic patterns in the scatter plot of Pythagorean triples»
https://pengkuanonmaths.blogspot.com/2025/08/parabolic-patterns-in-scatter-plot-of.html
https://www.academia.edu/143458666/Parabolic_patterns_in_the_scatter_plot_of_Pythagorean_triples
……
In this study, four parabolic functions were derived directly from the Pythagorean equation. These functions provide a mathematical description of the parabolic structures observed in the scatter plot of Pythagorean triples.
The scatter plot of basic Pythagorean triples reveals a highly regular arrangement on the (X,Y) plane. The plot of the basic Pythagorean triples shown in Table 1 occur precisely at the intersections of horizontal and vertical parabolas.
Figure 5 illustrates the superposition of the four derived parabolic functions on the scatter plot of all Pythagorean triples. The strong correspondence between the curves and the observed structures confirms the validity of the functional model.
In addition, the density distribution of the parabolas was computed, identifying regions of higher concentration. This analysis clarifies why the parabolic structures are so prominent in the scatter plot of all Pythagorean triples.
For more detail, please read «Parabolic patterns in the scatter plot of Pythagorean triples»
https://pengkuanonmaths.blogspot.com/2025/08/parabolic-patterns-in-scatter-plot-of.html
https://www.academia.edu/143458666/Parabolic_patterns_in_the_scatter_plot_of_Pythagorean_triples
