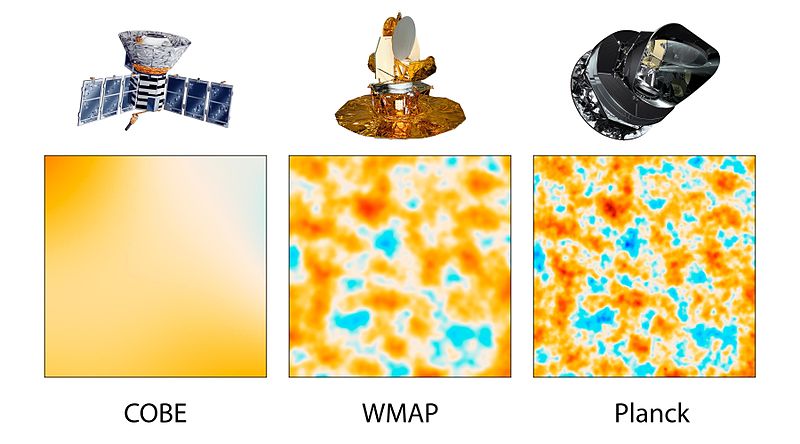
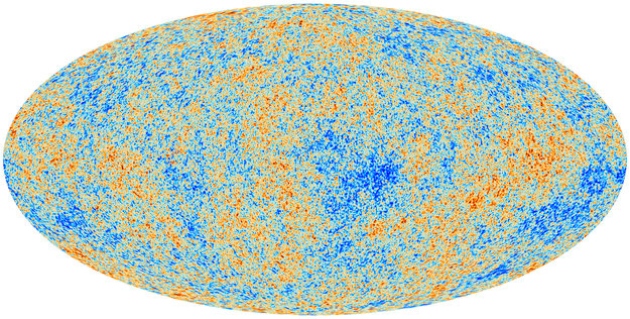
The Planck space telescope has produced the most detailed picture yet of the cosmic microwave background radiation (CMBR) [1].
NASA/JPL-Caltech/ESA
Detailed analysis supports the idea that \(10^{-32}s\), or there about, the Universe went into a phase of rapid expansion known as inflation. This rapid growth of the Universe explains why the Universe is so big and nearly flat, as well as providing an explanation as to why the CMBR temperature is uniform. More than this, the small anisotropies in the temperature are well explained by tiny quantum fluctuations in the early Universe that get blown-up by the inflationary phase. These small differences seeded the large scale structure of the Universe we see today.
ESA/PLANCK COLLABORATION
Hubble constant
From Planck we also know that the Universe is expanding today at a slightly lower rate than previous estimates have given. The Hubble constant is now revised to 67.3 kilometers per second per megaparsec, which makes the Universe about 80 million years older than WMAP data suggests.
Make up of the Universe
The new data has meant a revision in the proportions of “stuff” in the Universe:
Dark Energy – 68.3%
Dark Matter – 26.8%
Normal matter < 5%
Oddities in the CMBR
WMAP found and Planck has now confirmed, that there is an asymmetry between opposite hemispheres of the sky in the anisotropies of the CMBR. This suggests the rather unnatural possibility that there is a preferred direction in the cosmos. This does rule out some specific models of inflation, but the generic idea is still sound.

The cold spot
The CMBR cold spot is another strange feature that Planck has confirmed. This colder region of the CMBR, 70 µK colder that the average 2.7K was first discovered by WMAP. It is thought a possibility that the cold spot and the asymmetry maybe connected.
Links
Planck Science Team Home
Planck telescope peers into the primordial Universe, Nature, 21 March 2013
References
[1] Planck Collaboration, Planck 2013 results. I. Overview of products and results, submitted to Astronomy & Astrophysics, 2013.













