Preamble
So I have decided to create a few posts about some of the important mathematical ideas that I regularly encounter. The idea is to be rather informal and try to give a general feeling about these objects rather than a proper mathematical definition. I am hoping these posts will be readable to anyone with a reasonable high school education in mathematics. I will assume basic algebra and elementary geometry in the plane for example.
Please email me if you have something you would like me to cover.
So on to manifolds…
Introduction
Manifolds are an important notion in geometry and topology. Basically they are spaces that locally look like the much more familiar Euclidean spaces. This allows the well-understood notions on Euclidean spaces to be generalised to manifolds rather directly.
Coordinates
Recall that the space $latex\mathbb{R}^{n}$ for some integer $latexn$, can be understood by assigning an n-tuple \(x^{\mu}:=(x^{1}, x^{2}, \cdots , x^{n})\) of real numbers to each point; that is we can pick some coordinate system. The choice of coordinates is far from unique and a large part of geometry is related to the freedom in picking coordinates. We will not worry about changes of coordinates here.

Above we have a Cartesian coordinate system on the plane. Every point is assigned a pair of numbers.
It was Rene Descartes (1596-1650) who pioneered this analytic approach to geometry; today we honor him the term Cartesian when referring to coordinates. By employing coordinates, algebra and analysis can come to bare on question in geometry. This is in contrast to the axiomatic or synthetic approach that goes back to Euclid (circa 300 BC). The synthetic approach to geometry uses axioms, theorems and logical arguments to study spaces.
Manifolds
We can now describe the notion of a manifold, which is a higher dimensional analogue of a curve or a surface. A manifold of dimension \(n\) is a space, you can think of a collection of points, that locally looks like $latex\mathbb{R}^{n}$ for some integer \(n\). All curves in the two dimensional plane that do not intersect locally look like part of a line. All smooth surfaces in \(\mathbb{R}^{3}\), that is surfaces that do not have sharp kinks, edges, or points all locally look like the two dimensional plane, see figure below. Thus such surfaces are two dimensional manifolds. One should imagine being able to tear any small piece off the smooth surface, then being able to stretch it, push down any “hills” and push up any “valleys”” to end up with a flat piece of the 2-plane.
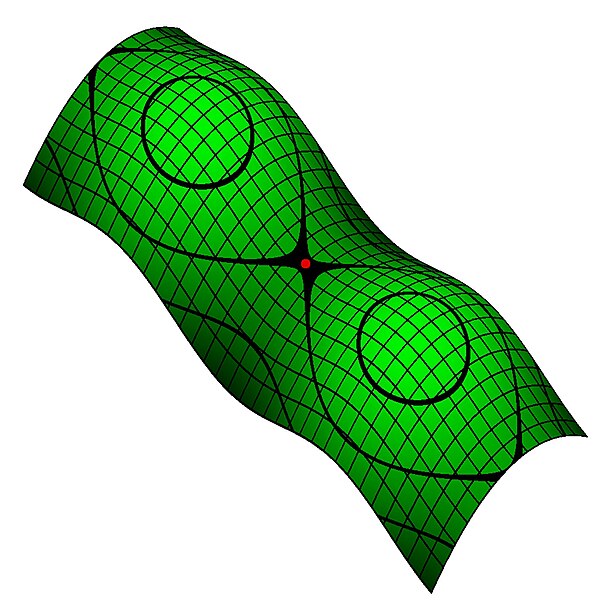
From Wikipedia
A little more formally, a manifold of dimension \(n\) can be thought of as being built up out of domains, which are open subsets of \(\mathbb{R}^{n}\). Intuitively, an open set is a set of points, in this case a subset of points belonging to \(\mathbb{R}^{n}\), such that any individual point can be displaced and still remain in the set. This gives a notion of points being “near” without the need for the notion of a distance between points. Such domains are commonly denoted as \(U \subset \mathbb{R}^{n}\). One can then “build” a manifold by patching these domains together, a bit like how one would make a patchwork quilt. It is how these domains are patched together that really defines the manifold.
In essence, the domains allows us to employ local coordinates when dealing with manifolds. Thus, one can build the theory of manifolds based on our understanding of the space \(\mathbb{R}^{n}\).
A quite familiar example to us all is the relation between a globe and a map. (I mean the common notion of a map, not the mathematical one!) The globe is a representation of the Earth (or any other planet) on the surface of the two sphere. Small pieces of the globe can always be represented as a map, which you think of as a piece of the two plane. Useful local coordinates on the maps can then be employed.

Image by Christian Fischer.
The picture to have in your mind when thinking about manifolds is the relation between a globe and a map. Small pieces of the globe can always be described by maps (pieces of the 2-plane). Moreover, the entire globe can be covered by a collection of maps: an atlas.

Etymology
The etymology of the word “manifold” is old English. The word literally means many folds. Today, generally the word has come to mean any object having many different parts or features. The use of manifold in the mathematical context is adapt, manifolds are generalisations of surfaces that are built up from many domains and have many features not seen on $latex\mathbb{R}^{n}$.
Not manifolds
It is also worth highlighting some spaces that are not manifolds. A very simple example would be a self-intersecting curve in the plane. Such a curve will have regions that look like “X”. At these intersection points we no longer have a manifold structure. Such spaces are known as manifolds with a singularity.
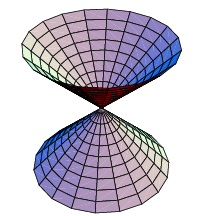
Image courtesy of Wolfram
The double cone above looks very much like a manifold apart from the point at which the two cones meet. Everywhere not near this apex locally looks like the plane. This is also an example of a manifold with a singularity.
Manifolds with a boundary are not manifold!. For example the finite cylinder has two circles which are one dimensional manifolds as it’s boundaries.

Applications
Manifolds can have a variety of extra structures on them. Indeed I have been very loose with the class of manifolds I have discussed here. Anyway, manifolds can have a differentiable structure on them meaning that we can do calculus on them. This is great for physics and indeed smooth manifolds are important in theoretical physics.
For example, smooth manifolds that come with a metric, that is a notion of distance on them, are at the heart of Einstein’s general relativity. Also, smooth manifolds also appear as the phase spaces in classical mechanics and these carry another interesting structure, that of a Poisson bracket.
I will say more about Poisson brackets in another post.







 Profs. Howard and Smith
Profs. Howard and Smith