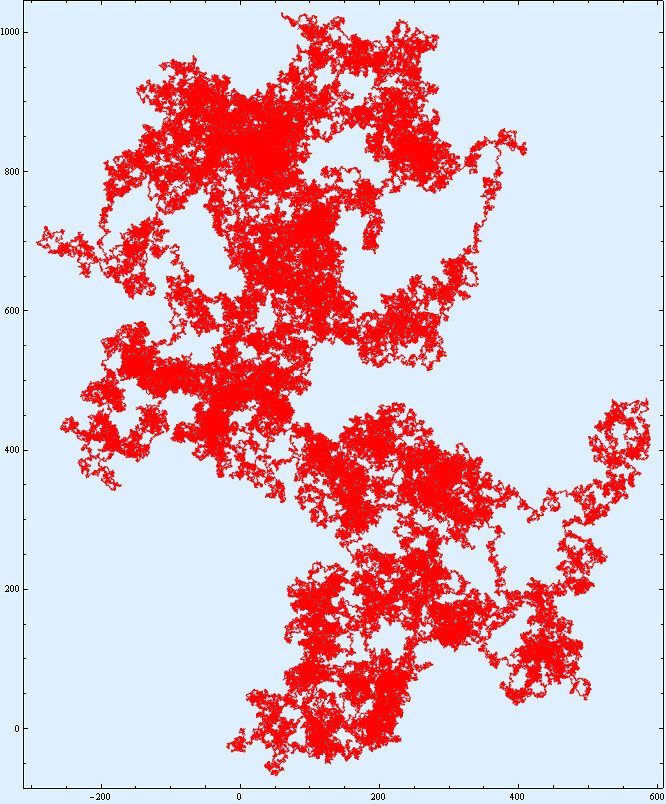
Random walks can be found throughout nature in many different contexts. For example they been used in ecology, economics, psychology, computer science, physics, chemistry, and biology. Above is an example of a (simple) random walk I created. There is 8 directions to this walk and 1000000 points.
The random walk above is an example of a Markov process, that means that the next step only depends on the present step. Such processes have “no memory”.
Random walks are closely related to Brownian motion, which is the physical phenomenon of minute particles diffusing in a fluid.
Random walks are examples of discrete fractals. They show self-similarity on large scales (such as in the picture above), but on the smaller scales the discrete nature of the grid becomes apparent. See the picture below.
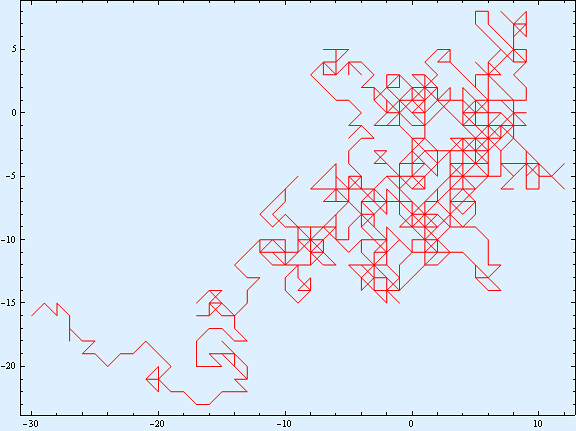
Here we have another random walk generated in exactly the same way as the previous one, but not just 1000 points. One can consider this as a “zoom in” on the random walk with a million points. The finite step size is apparent and the resemblance to genuine fractals is far less clear.
Links
Hi,
May I ask which algorithm you used to produce these runs?
Thanks!
Cheers,
Chris
The algorithm is basically
Start from a given point, which in this case is (0,0)
Pick one of eight directions (up, down, left, right, and the diagonals) at random. The algorithm I used has these choices equally weighted, but one could generalise that.
Draw a line of length one in that direction.
Loop
These are simple random walks that allow crossings, visiting the same point more than once and allows loops.